O USO DO WINPLOT COMO FERRAMENTA PARA O ESTUDO DAS TRANSFORMAÇÕES
LINEARES DO PLANO NO PLANO
Este post foi elaborado a partir de uma conferência que eu apresentei em 2009 no III ENCONTRO DOS ESTUDANTES DE MATEMÁTICA DA FAFIDAM (Faculdade de Filosofia Dom Aureliano Matos - Limoeiro do Norte).
1. O QUE É WINPLOT ?
O WINPLOT é um software, capaz
de representar diversos tipos de gráficos em 2D e 3D, desde pontos, funções nas
formas explícita, paramétrica e polar, dentre outras, bem como apresenta
algumas ferramentas para o desenvolvimento do Cálculo Diferencial e Integral. É,
também, um ambiente de jogo, quando é acessado o menu "adivinhar". Um
plotador gráfico ideal para
todos os níveis educacionais.
Desenvolvido
pelo professor Richard Parris, da Philips Exeter Academy, o Winplot é um dos principais
softwares da linha Peanut Softwares, que contém uma
lista de vários outros softwares matemáticos.
Programa
simples, mas poderoso, podendo executar grande número de tarefas. Outra de suas
vantagens é ser gratuito, podendo por isso ser utilizado sem problemas por
professores e alunos do Ensino Fundamental, Médio e Superior. Neste sentido
achamos útil que este programa seja difundido para professores de matemática,
trazendo com isso uma possibilidade maior de interação às aulas de matemática.
Nosso propósito, a partir de agora, é usá-lo como uma ferramenta de apoio para um tópico de Álgebra Linear, as transformações do plano no plano.
2. Transformações
do plano no plano:
Nesta apresentação
serão abordados os aspectos de investigação matemática com apoio do módulo “Mapeador” do Winplot para uma melhor visão geométrica das transformações do
plano (R2)
no plano. Veremos assim, que, por exemplo uma expansão, uma rotação e certas
deformações podem ser descritas por transformações lineares.
3. Mapeador do Winplot – Plano xy
3. Mapeador do Winplot – Plano xy
4. TRANSFORMAÇÃO
LINEAR
Definição: Sejam V e W dois espaços vetoriais. Uma transformação (ou aplicação) T: V→W é dita linear se forem verificadas as relações:
Definição: Sejam V e W dois espaços vetoriais. Uma transformação (ou aplicação) T: V→W é dita linear se forem verificadas as relações:
i) T(u + v) = T(u) + T(v);
ii)
T(au) = aT(u), sendo a um número real e u,
v elementos de V
Se V = W e T é uma transformação linear, então T é chamado de operador linear sobre V.
Se V = W e T é uma transformação linear, então T é chamado de operador linear sobre V.
Exemplo 1: A aplicação T: R2 → R2 definida por T(v) = kv é um operador linear de R2, chamado de homotetia de razão k de R2. Se k > 1, dizemos que T é uma dilatação ( ou expansão) e se 0 < k < 1, dizemos que T é uma contração.
Observe o efeito
geométrico obtido com essa transformação. A homotetia (contração) “diminuiu” o
tamanho do triângulo original. O primeiro triângulo tem base e altura de
medidas 4 unidades de comprimento e 3 unidades de comprimento, respectivamente,
enquanto o segundo tem base e altura de medidas 2 unidades de comprimento e 1,5
unidades de comprimento, respectivamente.
Exemplo 2: O ponto P’ é o ponto
simétrico do ponto P em relação à reta r quando r é a mediatriz do
segmento
PP’. Se P pertencer a r, então o seu simétrico em relação a r é ele próprio.
A aplicação T: R2 →
R2
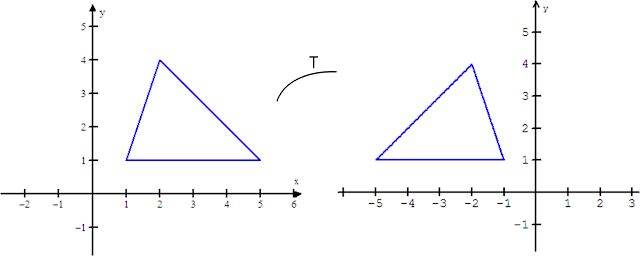
definida por T(x,y) = (x , –y ) é uma reflexão em torno do eixo x. Na opção Função|Nova, digite U(x,y) = x e V(x,y)
= –y e plote o mesmo
triângulo do exemplo anterior com cor azul.
Agora, considere a
aplicação T: R2 → R2 definida por T(x,y)
= ( –x , y ) que é uma reflexão em torno do eixo y. Na opção Função|Nova, digite U(x,y) = –x e V(x,y)
= y e observe a nova
posição do triângulo.
Exemplo 3: A aplicação T: R2 → R2
definida por T(x,y) = (x + αy, y) é chamada cisalhamento
horizontal de fator α . Na
opção Função|Nova, digite U(x,y)
= x+2y e V(x,y) = y
e plote o mesmo quadrado do exemplo anterior. Observe o que ocorre com o
quadrado.
A aplicação T: R2 → R2
definida por T(x,y) = (x , αx + y) é chamada cisalhamento vertical
de fator α . Na opção Função|Nova, digite U(x,y)
= x e V(x,y) = 2x + y e plote o mesmo quadrado do
exemplo anterior. Observe o que ocorre com o quadrado.
T(x,y) = (xcosθ – ysenθ, xsenθ + ycosθ).
Digitando
U(x,y) = xcos(a) – ysin(a) e V(x,y) = xsin(a) + ycos(a)) e fazendo o parâmetro “a” variar num
determinado intervalo, podemos visualizar a rotação de uma figura em torno da origem dinamicamente. Por
exemplo, construa um quadrado com os seguintes segmentos:
de (0,0) até (1,0), de
(1,0) até (1,1), de
(1,1) até (0,1) e
de (0,1) até (0,0). Na
opção Anim | Parâmetros A-W ,
digite 0 e clique em “def-L” e digite 2pi e clique em “def-R” e, em seguida,
clique em “auto
cícl”.
Atenção: Em breve postarei um vídeo ensinado passo - a - passo esta atividade!